本次作业以解析表达式并简化后输出为核心任务。

主要的实现过程为：
预处理->解析->化简->输出

迭代过程综述

预处理的迭代

第一次作业：空白字符与正负号
第二次作业：递推函数
第三次作业：自定义函数

解析的迭代

第一次作业：常数因子、幂函数因子、表达式因子
第二次作业：三角因子 第三次作业：求导因子

化简的迭代

第一次作业：多项式的加乘幂
第二次作业：含三角函数的加乘幂及其化简
第三次作业：求导运算

输出的迭代

第一次作业：输出多项式
第二次作业：输出含三角函数的表达式 第三次作业：无

第一次作业

刚刚走进面向对象课堂的第一天，就被HW1深刻地击溃了。
不同于其他同学只是担心可扩展性不够强而不肯动笔————我的大脑是完全空白的。

我知道是这个道理，但是到底怎么写？

我认为理解递归下降实际运行的关键，在于深刻理解lexer的执行逻辑，lexer作为parser的属性，是唯一确定的，当我解析完成，lexer也就走完了。解析的过程就是lexer的前进过程。

而我们做的事情，就是根据读取expression，自行出构建一个新的、有结构的Expr。

接下来的toPoly便也是递归下降的一种体现。我已经知道最小单元Mono与Power有它具体的toPoly()方法，那么我就可以采用递归下降，对每一个类只着眼于它自身的运算过程。

代码量

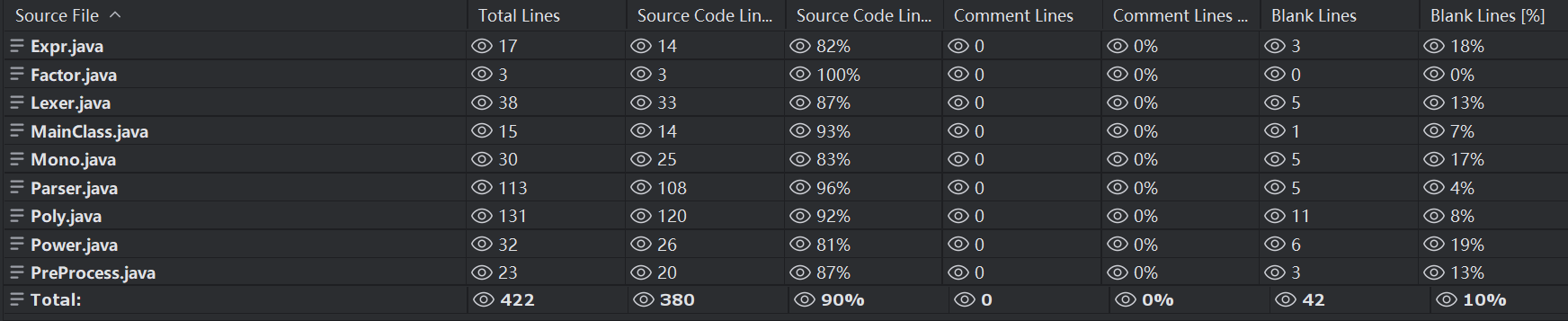
可以看出核心代码在于解析Parser与化简Poly这两个类中。

UML类图

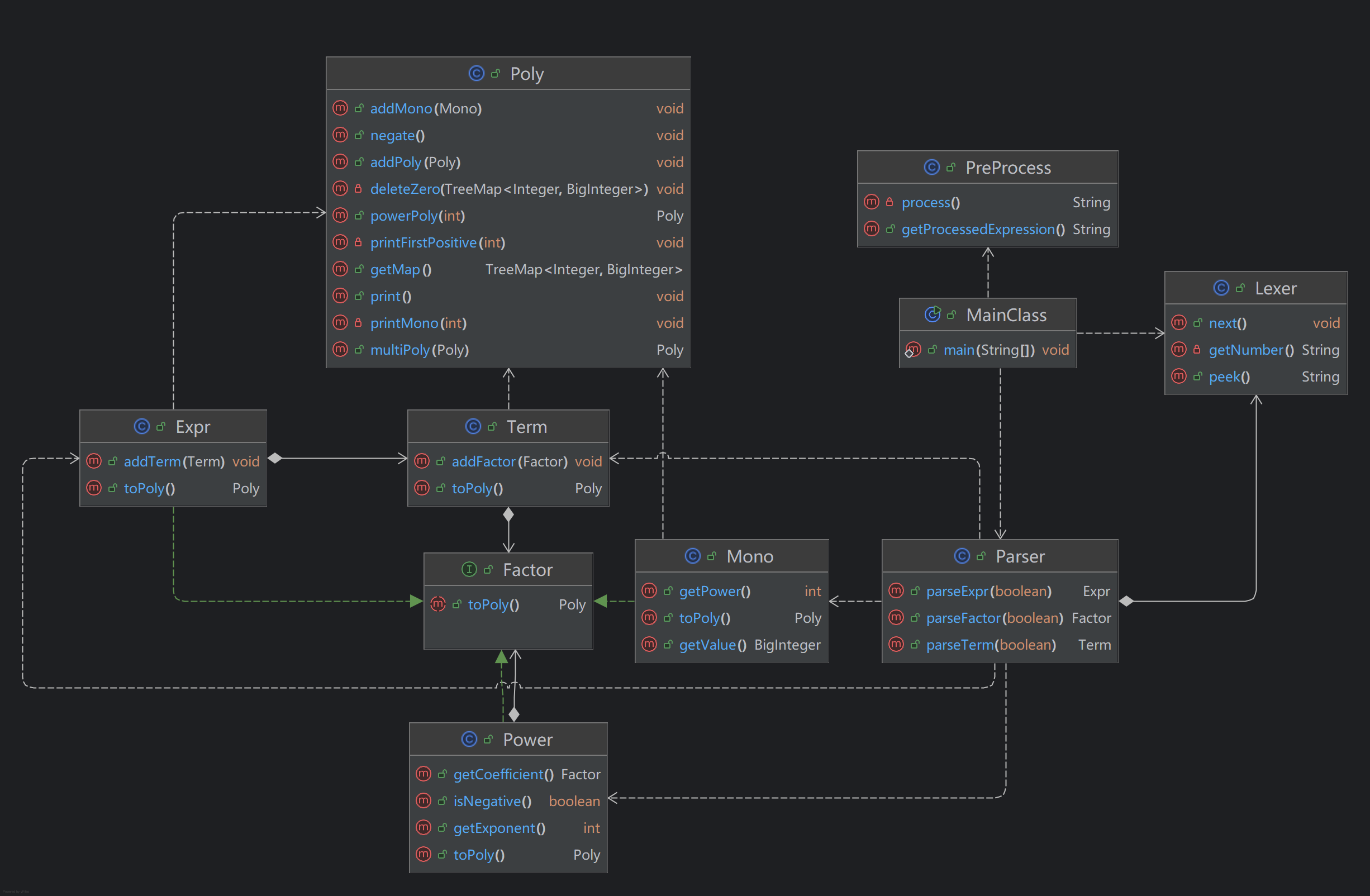
方法数则是Poly类遥遥领先，不过都是加、乘、幂、去零、取反、输出等基本方法

复杂度

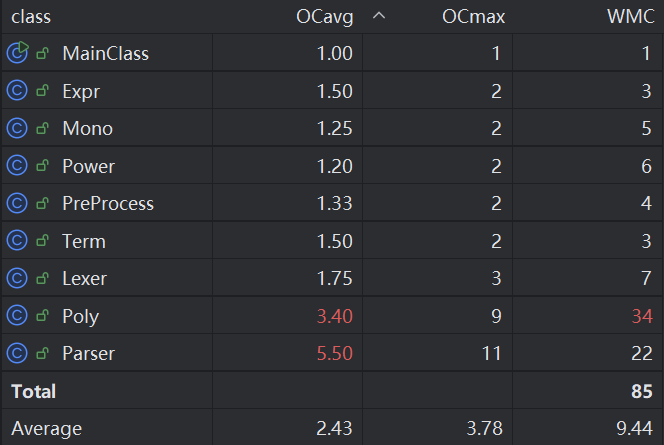
同样的，Parser与Poly的复杂度是远高于其他类的。

类的设计

PreProcess为预处理类，直接把空格与连续正负号解决掉，简化Parser的处理。

Mono类与Power类则对应了最小解析单元（因子中的常数，幂函数与表达式因子），这里将常数与幂函数都归为Mono类是很方便的。

第二次作业

如果说第一次作业是从零到一的突破，那么第二次作业可能就是从1到x的蜕变。
三角因子本身的复杂性太强，不能像之前一样简单的归类，更没有统一的计算方法。

曾经Poly里的加与乘，如今全部都复杂起来了！
我们只能进行重构。

对于加法，我们没有曾经直接看x的幂次来进行合并同类项的简单解法，
因此只有写出同类项判别方法，才能实现加法的简化

对于乘法，我们需要先实现最小单元之间幂函数幂次与三角因子幂次的累积
再进行所有乘积项的求和

代码量

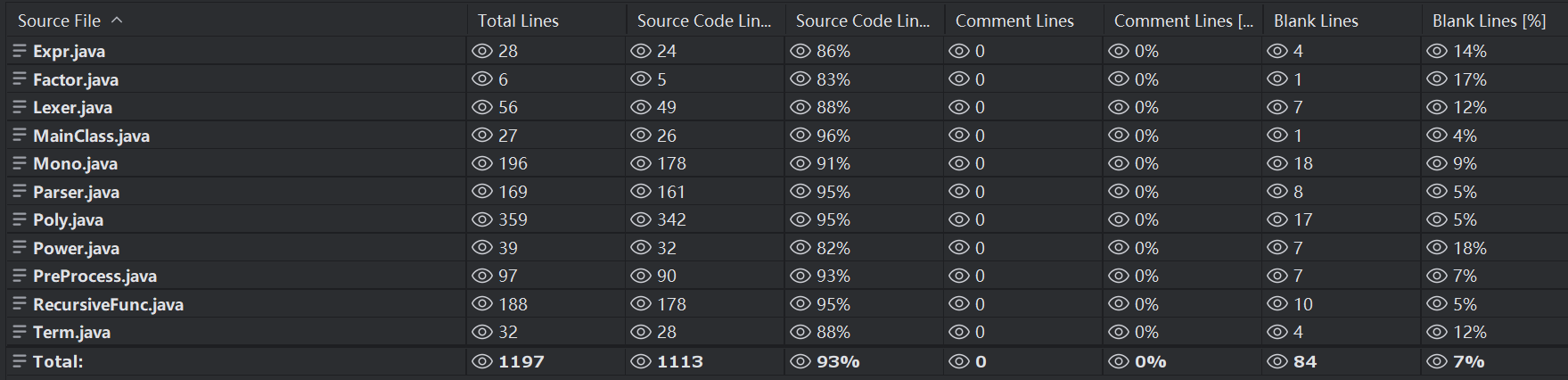
较上次作业新增了近800行，其中parser变化不大，而Mono与Poly代码量激增
此外还有新增的类: 递归函数RecursiveFunc

UML类图

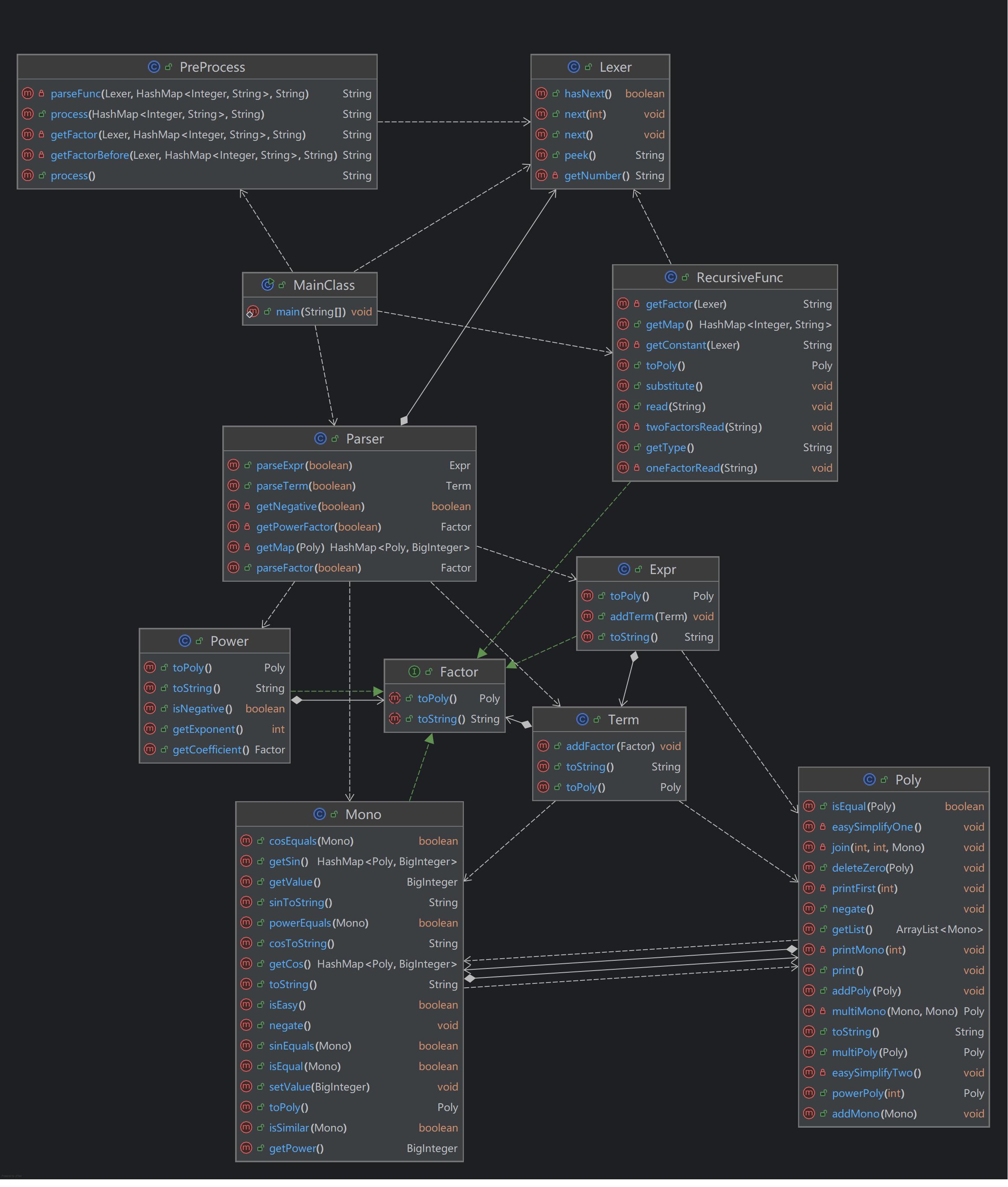
我调整了类的相对位置使之更加清晰。

图片从上到下分别是函数预处理，表达式解析，表达式化简运算与输出

复杂度

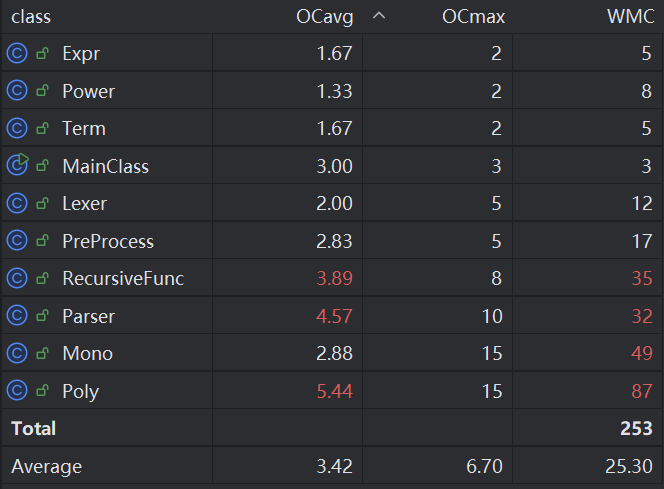
Parser与Poly不出意外的高复杂度。
但是递推函数类的复杂度异常的高，我承认我当时采用的方法过于粗暴。
后续果然发现了bug，只是到了第三次作业的环境中才得以体现出来。

类的设计

Mono类秉承着原来解析的最小单元的地位，现在的它，是一个除了表达式因子以外可以包罗万象的Factor,含有常数，幂函数的幂次，三角函数的HashMap<Poly, BigInteger>。

因此，他也仍然是最终运算的最小单位，充当最终表达式中的项（Term）。

Poly则是所有Mono的和，用ArrayList实现。

接下来是RecursiveFunc类。我将函数翻译作为了预处理操作的一部分，实现了在解析开始之前就解决掉了所有的函数问题。这个类的核心作用就是根据已知信息，直接获得一个从0到5的函数Map。

接着process类也将被重写，并增添替换操作。

第三次作业

经历了HW1的无力茫然与HW2的大刀阔斧
站在HW3面前的你，
应当充满了决心！

代码量

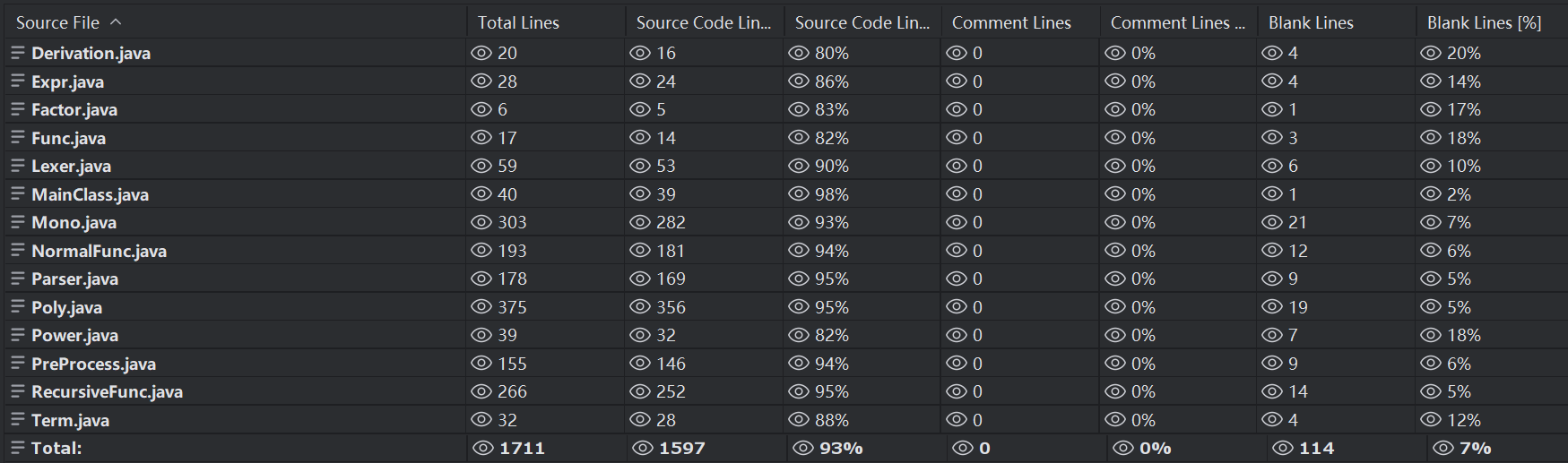
代码行数增加的并不多

主要内容是新类的添加，更多的函数代入操作以及求导计算

UML类图

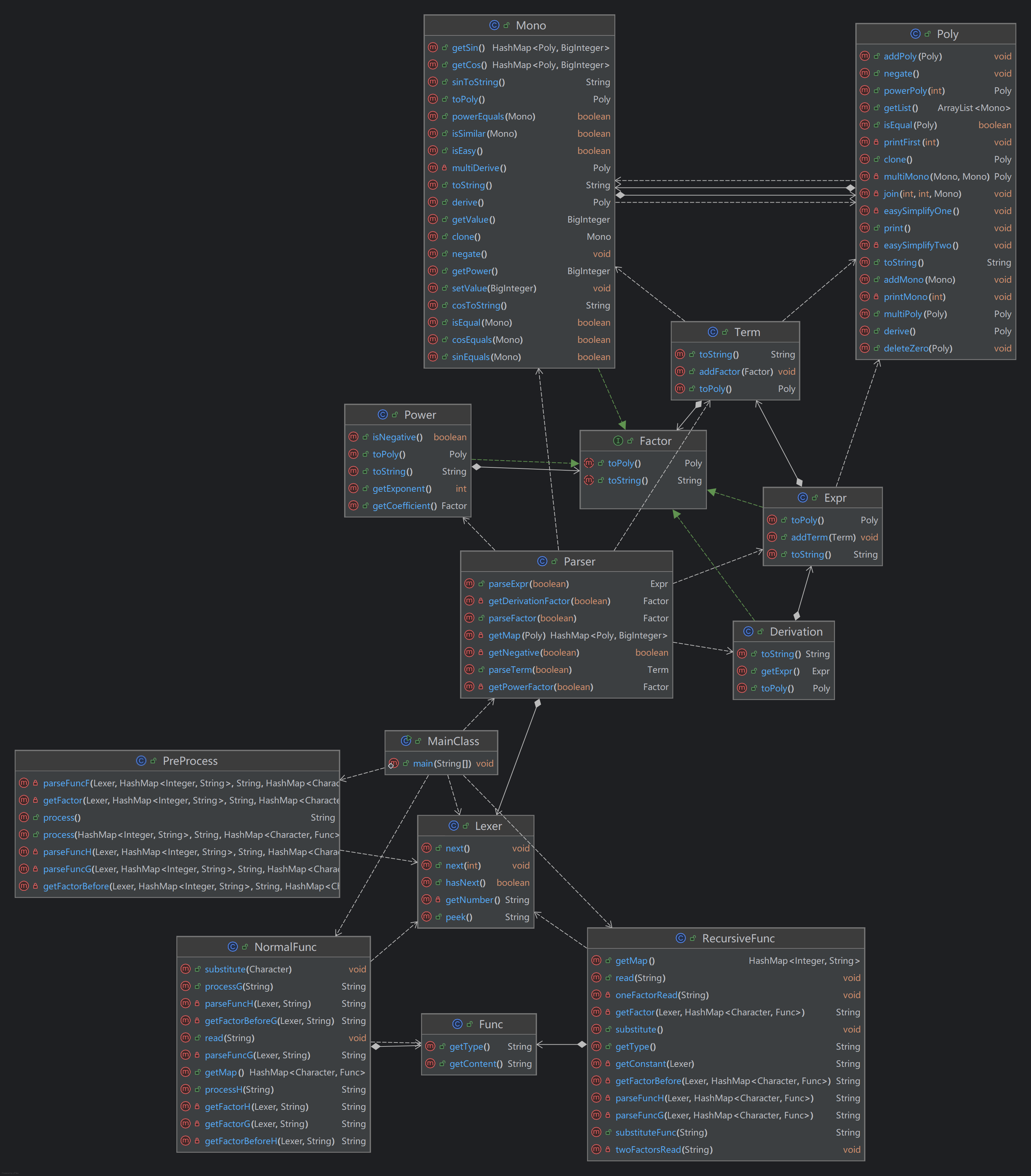
相较于hw2，在Factor上新增了求导因子，在预处理上新增了NormalFunc以及一个数据功能类Func。

复杂度

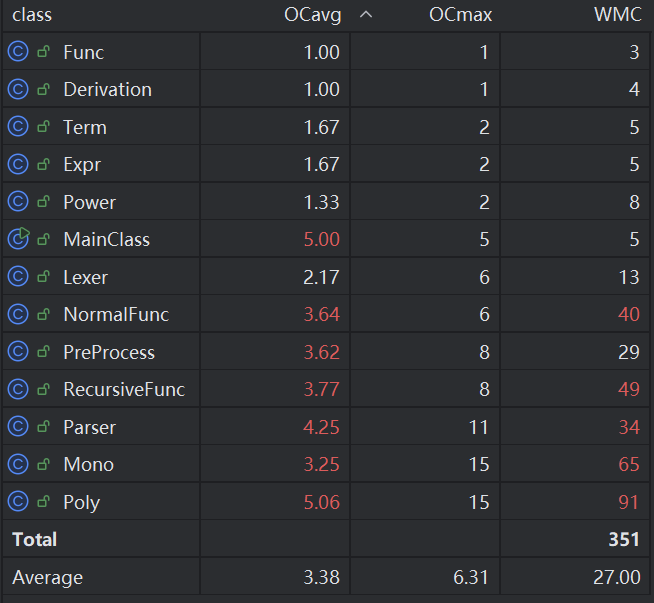
类的设计

Derivation类作为一个Factor，需要toPoly()方法，只需要将expr先toPoly，在调用Poly()的derive方法。

NormalFunc类的设计与RecursiveFunc的思路基本一致，只是少了递推这一步。

可扩展性

• 函数的扩展： exp函数，只需对Mono类添加一个Poly属性，用于记录指数。 ln函数，同理，只需记录真数。
• 变元的扩展： 只需Mono的power变为power1和power2，分别作为两个变元的幂指数

BUG

• 第一次作业 0 bug

• 第二次作业 强测 0 bug 互测 2 bugs 错因是在截止前20min才意识到忘记处理sin(0)与cos(0)，这会对性能产生极大的损害。
  而在优化了这一点之后，由于从未对数字0 ^ 0有过定义，sin(0)^0就变为了0
  而在时间紧迫的情况下，我也没来得及用评测机进行评测。提交截止之后，评测机很快就跑出了该问题。

  另一处bug是犯了很多次的二重循环初始化错误，修改了之后还是遗漏了一个地方。

  正如教程所说，这两个点都是高行与圈复杂度的类（Mono与Poly）所出现的问题，耦合性强，不易被发现。

  若想降低复杂度，也就是解耦合，就需要做好一些预先的规划，将谁该做什么事分清楚。不过Poly与Mono的耦合度高，个人认为是较难避免的。因为Poly里会用到Mono的同类项判别方法，这个方法中又会涉及会Poly(三角函数内)的equal方法，这一equal方法又会归结于Mono

  或者说，Poly跟Mono的关系，就很有一种Expr与Factor的感觉。

• 第三次作业 0 bug

评测机搭建

这三周以来很有成就感的一件事，就是我终于主动尝试着搭出了自己的评测机！

check.py比对

利用了sympy库中的函数
python库就是神通广大（）

data.exe数据生成

核心内容

我使用的是随机暴力生成的方法

构建的逻辑就是递归下降咯

printExpr->printTerm->printFactor

bat批处理程序运行

学习了一些基本运行语句：
java -jar .jar python .py .exe

利用了一些基础的重定向。

BUG分析

首先是评测机暴力跑数据，通过简化数据点抓住核心问题数据，再定位到代码的具体漏洞位置。这一招在hw2中就大杀四方，获得了5个不同质的bug。

其次便是手动构造边界数据，尤其是0,0次幂，1次幂等特殊情况，多加测试。

遗憾的是，由于代码阅读能力不够强，我常常没有心力去认真观察他人的代码来寻找bug。

优化

输出符号优化

hw1便涉及到的，存在正项则提前

sin cos正负号优化

对于因子内部全为负的三角因子，我会直接对该Poly使用negate方法，使其含有正项，从而缩短长度

这一处理在某种程度上也统一了一些格式，便于同类项的判断

不足之处在于还是不能用于全面的判断两个Poly是Opposite的，例如1-x与x-1，便不会经过处理，从而后续不会被判定为同类项

改进： 我们可以采用相加等于0的方法来判断Poly的isOpposite

sin^ 2+cos^ 2 sin^ 2-cos^ 2 sin^ 4-cos^ 4

为了能够处理嵌套括号内的该类内容，我选择了在每次addPoly()时都加以判断，并且提取了公因式（不过无法处理幂次的公因式，比如sin(x)^ 3+cos(x)^ 2*sin(x)）。

一处问题：在二倍角过程中，我改变了三角因子的Poly。这一行为决定了我们必须使用深克隆！

另一处问题：过于频繁与紧急的匹配会导致贪心，例如sin(x)^ 2 - cos(x) ^2 + cos(x) ^2, 便会被我使用二倍角，从而闹出笑话。

改进：在最后再处理化简工作，至于嵌套，可选择遍历内部嵌套进行化简。

心得体会

作为第一章，面向对象的思想已经比较清晰地发散开来了。递归下降这一算法，本身就是十分符合面向对象的思维方式，每个类做好自己的算法，问题一定能得到解决。

hw2是很不错的一次体验，虽然是最辛苦的一周，但是无畏地向前探索，不合适就重构的勇气是很宝贵的。

搭建评测机也是很奇妙的一次体验。自主学习的收获总是刻骨铭心。

未来方向

个人认为递归下降的内容如果能在理论课上详细结合代码来讲解运行逻辑，可能hw1就不会显得那么痛苦（）

但是这种痛苦也是有益的，至少它让我从懵懂的第一周里清醒过来：

面向对象的挑战，已然开始。